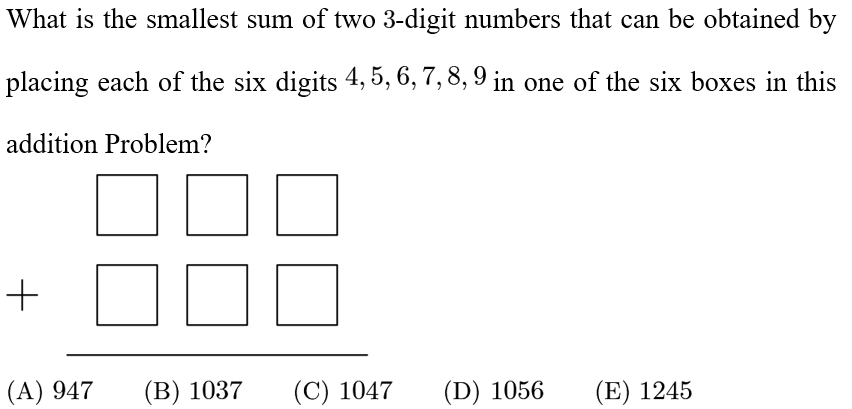

Answer: C
Solution:
One is 468, the other is 579. 468+579=1047.
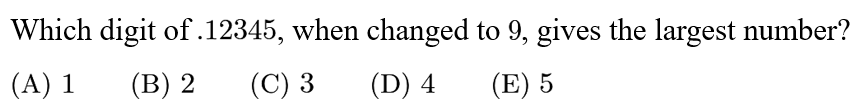
Answer: A
Solution:
When dealing with positive decimals, the leftmost digits affect the change in value more. Thus, to get the largest number, we change the 1 to a 9.
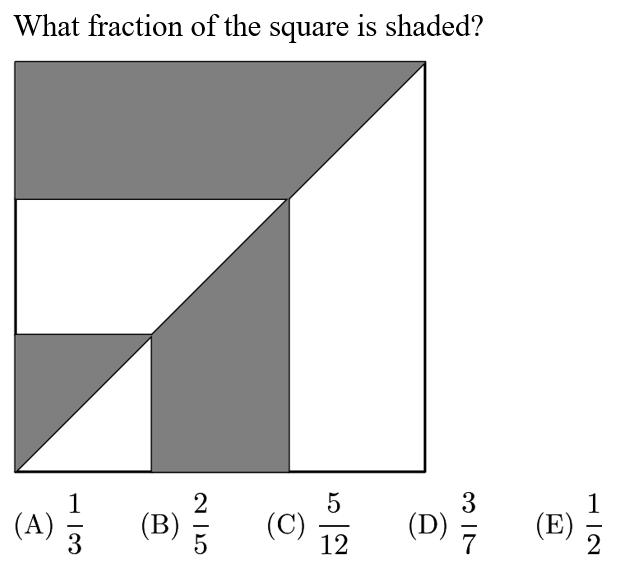
Answer: E
Solution:
Reflecting the square across the diagonal drawn, we see that the shaded region covers exactly the unshaded region in the original square, and thus makes up 1/2 of the square .

Answer: E
Solution:
For integers, only the units digit affects the units digit of the final result, so we only need to test the squares of the integers from 0 through 9 inclusive. Testing shows that 8 is unachievable, so the answer is E.

Answer: B
Solution:
Clearly, 0.4<0.48017<0.5; 0.5*0.5*0.5=0.125, so B is the answer.
Since 0.48017 is quite close to 0.5, we can look for the answer choice that is just below 0.5*0.5*0.5=0.125 , which would be B .
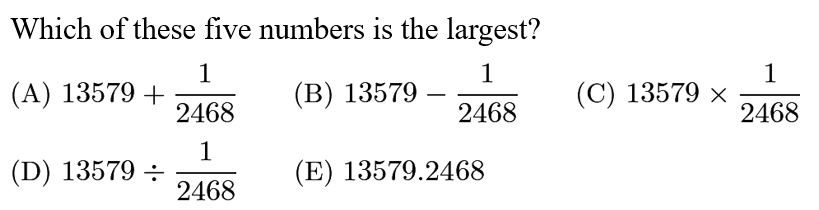
Answer: D
Solution:
The options given in choices A, B, and E don't change the initial value (13579) much, the option in choice C decreases 13579 by a lot, and the one given in choice D increases 13579 by a lot.

Answer: C
Solution:
First we try for a positive product, meaning we either pick three positive numbers or one positive number and two negative numbers. It is clearly impossible to pick three positive numbers. If we try the second case, we want to pick the numbers with the largest absolute values, so we choose 5, -3, and -2. Their product is 30.

Answer: D
Solution:
After the price reduction, the sale price is 80*(1-0.25)=60 dollars. The tax makes the final price 60*1.1=66 dollars.

Answer: D
Solution:
We just count to find that there are 5 students in the C range.
There are 15 total, so the percentage is 5/15=33.3%.
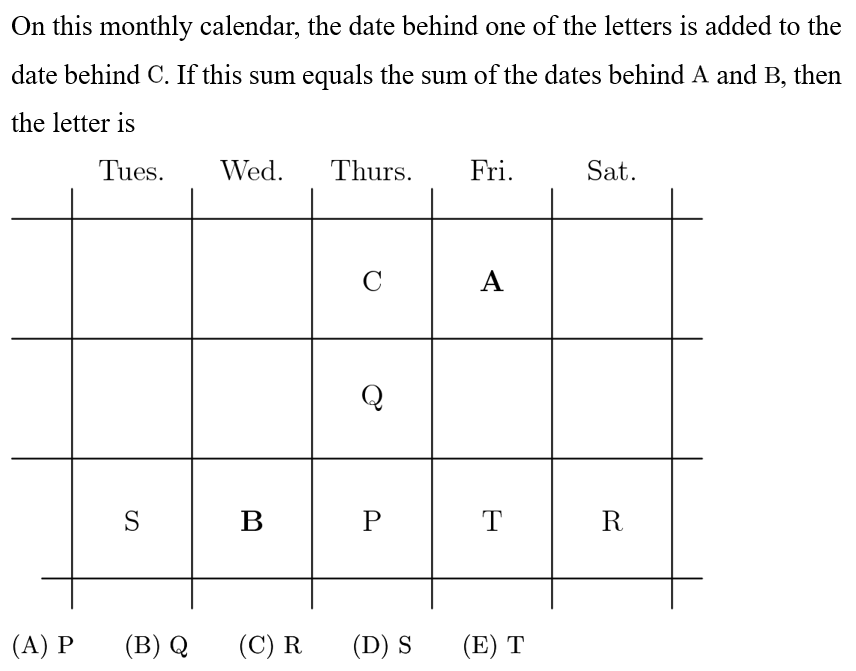
Answer: A
Solution:
Let the date behind c be x. Now the date behind A is x+1, and after looking at the calendar, the date behind B is x+13. Now we have x+1+x+13=x+y. for some date y, and we desire for y to be x+14. Now we find that y is the date behind P.
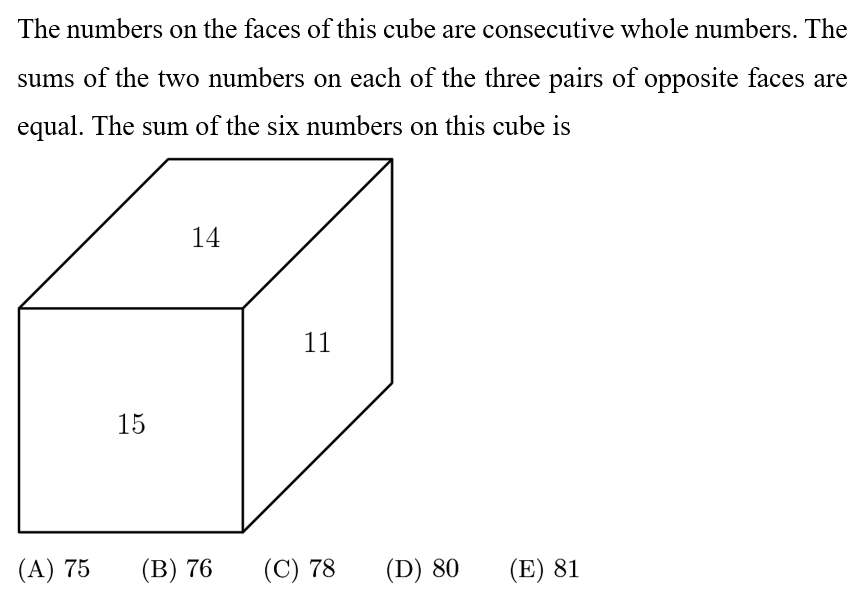
Answer: E
Solution:
The only possibilities for the numbers are 11,12,13,14,15,16or10,11,12,13,14,15..
In the second case, the common sum would be (10+11+12+13+14+15)/3=25, so 11 must be paired with 14, which it isn’t. Thus, the only possibility is the first case and the sum of the six numbers is 81.

Answer: B
Solution:
For each choice of the thousands digit, there are 6 numbers with that as the thousands digit. Thus, the six smallest are in the two thousands, the next six are in the four thousands, and then we need 5 more numbers.
We can just list from here:5247, 5274, 5427, 5472, 5724.

Answer: C
Solution:
After the first ounce, there are 3.5 ounces left. Since each additional ounce or fraction of an ounce adds 22 cents to the total cost, we need to add 4*22 to the cost for the first ounce.
So, the total price is 30+4*22=118 cents.

Answer: B
Solution:
The total number of balls in the bag must be 4*6=24. so there are 24-6=18 green balls .
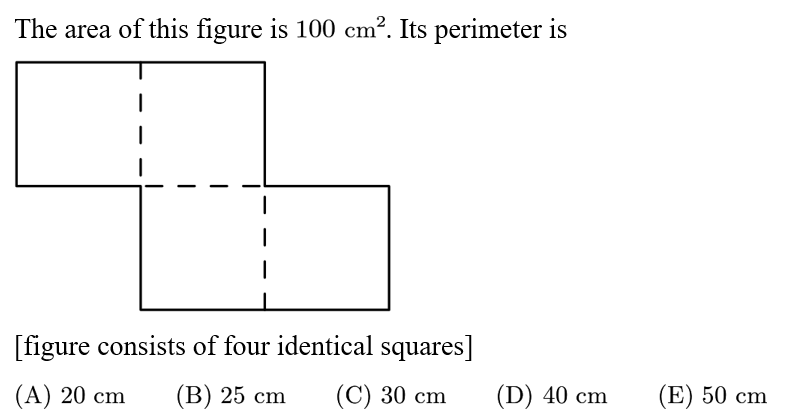
Answer: E
Solution:
Since the area of the whole figure is 100, each square has an area of 25 and the side length is 5.There are 10 sides of this length, so the perimeter is 10*5=50.
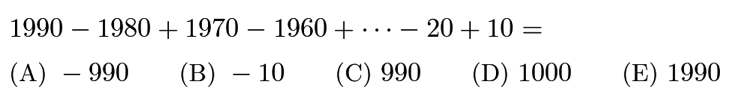
Answer: D
Solution:
In the middle, we have …+1010-1000+990-…, If we match up the back with the front, and then do the same for the rest, we get pairs with 2000 and -2000, so these will cancel out. In the middle, we have 2000-1000 which doesn't cancel, but gives us 1000.

Answer: A
Solution:
This is a 1 yard by 20 yard by 1/12 yard sidewalk, so its volume in yards is 1*20*1/12=5/3. Since concrete must be ordered in a whole number of cubic yards, we need 2.

Answer: C
Solution:
In addition to the original 12 edges, each original vertex contributes 3 new edges.
There are 8 original vertices, so there are 12+3*8=36 edges in the new figure.

Answer: B
Solution:
p is a person seated, o is an empty seat. The pattern of seating that results in the fewest occupied seats is opoopoopoo...po we can group the seats in 3s opo opo opo ... opo
there are a total of 40 groups.

Answer: A
Solution:
Let s be the sum of all the incomes but the largest one. For the actual data, the mean is (s+98000)/1000, and for the incorrect data the mean is (s+980000)/1000. The difference is 882.

Answer: B
Solution:
We just use the definition to find the first number is 1/4.

Answer: B
Solution:
If this is the case, then if there were only 99 pieces of candy, the bag would have gone around the table a whole number of times. Thus, the number of students is a divisor of 99. The only choice that satisfies this is choice B.
Answer: B
Solution:
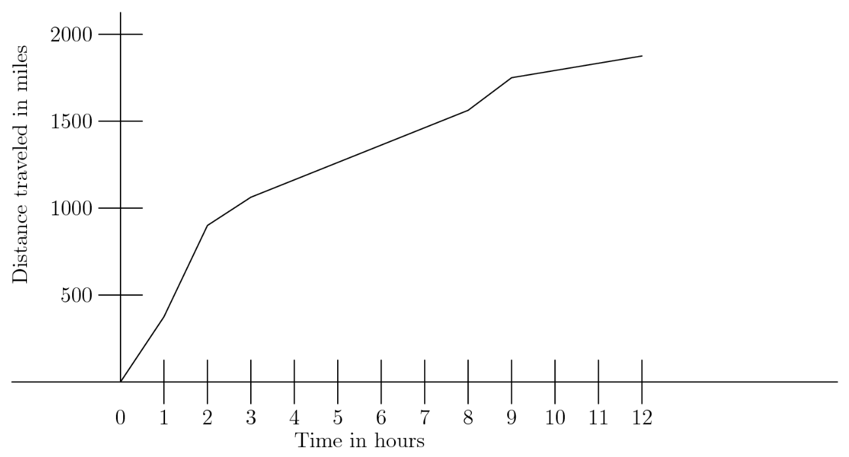
The time when the average speed is greatest is when the slope of the graph is steepest. This is in the second hour.
Answer: C
Solution:
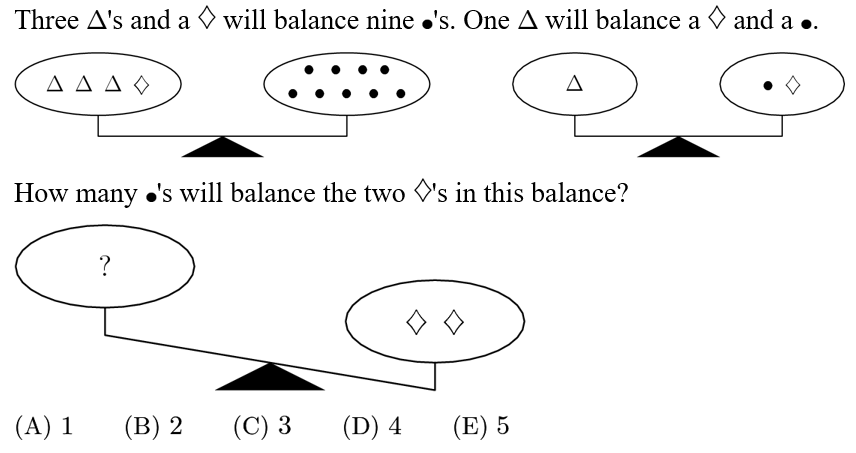
For simplicity, suppose triangle=a, trapezoid =b, and dot =c. Then, 3a+b=9c, a=b+c and we want to know what 2b is in terms of c. Substituting the second equation into the first, we have 4b=6c => 2b=3c. Thus, we need 3 dots.

Answer: C
Solution:
Case 1: At least one square is a vertex: suppose one of them is in the upper-left corner. Then, consider the diagonal through that square. The two squares on that diagonal could be the second square, or the second square is on one side of the diagonal.
In this case, there are 2+3=5 distinct squares.
Case 2: At least one square is on an edge, but no square is on a vertex: There are clearly two edge-edge combinations and one edge-center combination, so 3 squares.
In total, Its 5+3=8.
AMC培训、答疑,请联系微信 / 电话:136 1118 1627
艾蕾特教育 @Elite Edu, 在这里,